Autechre’s Critical Theory Generator for the Lovebytes 2001 catalog

A little while ago, I had a flood and — among other things — all my vinyl got damaged. Packed alongside the vinyl, I found the catalog (also water damaged) for Lovebytes 2001 — an electronic arts festival which ran in the early 2000s. (I guess it must have been thrown in as some promo gear along with something I purchased from Warp at the time because I didn’t make it to the festival itself.)

A water-damaged Lovebytes 2001 catalog.

Flicking through the catalog, it’s a lovely snapshot of the time — reminiscent of zine culture — that carries the enigmatic optimism the scene seethed with: there are shorts in there about Eric Singer, interviews with Jeremy Bernstein, and articles about Oval written in fonts too small to read.

Late in the catalog, there is a verbose treatise that discusses the works of Booth, Brown, Autechre, and Gescom. I’d long wondered what it was and I only just stumbled across the answer: it’s text from a “critical theory generator” made by Autechre (with Max of course) to generate their “manifesto for the lovebytes 2001 catalogue”. The explanation was originally posted in a Q&A microsite (q 4 ae) on the Warp Records website. It’s hard to find again on archive.org, but some of the questions/answers have been reposted on WATMM:

https://forum.watmm.com/topic/90626-what-you-shouldve-asked-in-aaa/page/2/#comment-2444177

I didn’t manage to find a digitised version of this online, so I’ve scanned it and uploaded it to archive.org for posterity: https://archive.org/details/autechre-critical-theory-generator-for-lovebytes-2001

Teaching Max to play Dance Dance Revolution

I’ve been playing some old games with OpenEmu recently, and got hooked on the idea of automating DDR game input by reading content from the screen with Max and sending virtual keystrokes back to OpenEmu. Here’s a quick example of what I ended up with:

Max plays some of the more difficult levels of the game.

The backstory…

It all started when I found some PlayStation ‘dance mat’ controllers (like these) that were made for the Dance Dance Revolution PSX game. I have an original PSX and a copy of the game that are boxed up somewhere, so I tracked down an ISO of the game (and connected the mats to the computer with a PSX to USB converter) to try them out with an emulator instead. The mats had been folded up for years and no longer worked very well, but the futile exercise got me thinking about how you might create a virtual DDR-bot with Max that could ‘read’ the arrow information from the screen to trigger button presses automatically.

The idea took several approaches before the system was confident enough to know how to play. But, as it turns out, we can get surprisingly far with some primitive computer vision strategies.

Here’s how I built it…

OpenEmu

Setup

The first thing that is worth doing is making OpenEmu’s emulation larger. The size of the game window (at 1.0x) in OpenEmu is 300×240 (which is a little small on my 2560×1440 display), so I elected to upscale the window in OpenEmu a little bit (2.0x) to make it a little more ‘readable’ on my screen.* As we’re going to use Max to observe the game though, this means that we’re actually asking it to watch 4.0x as many pixels (given that it is doubled in width and height… but my 2013 machine seems to cope OK).

* As well as adjusting the scale of the window, OpenEmu lets you apply filters the emulation, so I’ve kept this as Pixellate to preserve hard edges by duplicating pixels without smoothing. (Nearest Neighbour would also be fine). We’ll re-downscale this in Max with interpolation off (jit.matrix 4 char 300 240 @interp 0) to reduce our pixel crunching.

While the game window is now upscaled to 600×480, the actual location of the game window on my screen starts at (2, 45) given the border of the windows and menu bar in macOS Catalina. We’ll therefore ask Max to watch the desktop with: jit.desktop 4 char 600 480 @rect 2 45 602 525

Getting the Game Screen Into Max

Getting the game screen into Max was fairly easy, but the first time you use jit.desktop you need to explicitly give it permission to capture the screen.

Once the permissions are granted in System Preferences, we are able to capture the game window. Progress.

One of the first things I noticed after doing this is that there are a number of visual cues around the screen which might be helpful to time the simulated keystrokes. One of these was the way that the target arrows pulsed in time with the music.

The monochromatic arrow areas pulsing in time with the music.

At this point, I started working in parallel on being able to trigger OpenEmu from Max.

Triggering Key Presses in OpenEmu

A Major Catch

This part of the process ended up being a little more involved, due to the way that OpenEmu captures keyboard events. The initial plan was to ask Max to trigger keyboard input using something like 11olsen’s 11strokes object. Unfortunately, OpenEmu captures keyboard input events a lot lower than Max can send them, so it won’t respond to AppleEvents or simulated keyboard input.

OSCulator-in-the-Middle

The solution was to creating a virtual joystick with OSCulator, and have Max pipe OSC encoded instructions to it that could be converted to HID events.(See https://github.com/OpenEmu/OpenEmu/issues/1169). To create the virtual joystick, you need to install a system extension.

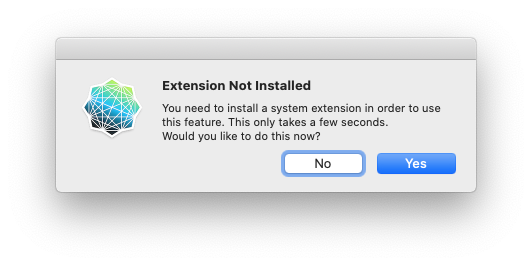
After installing OSCulator’s Virtual Joystick system extension and setting up the OSC routes, I was able to map OSC messages to HID button events.

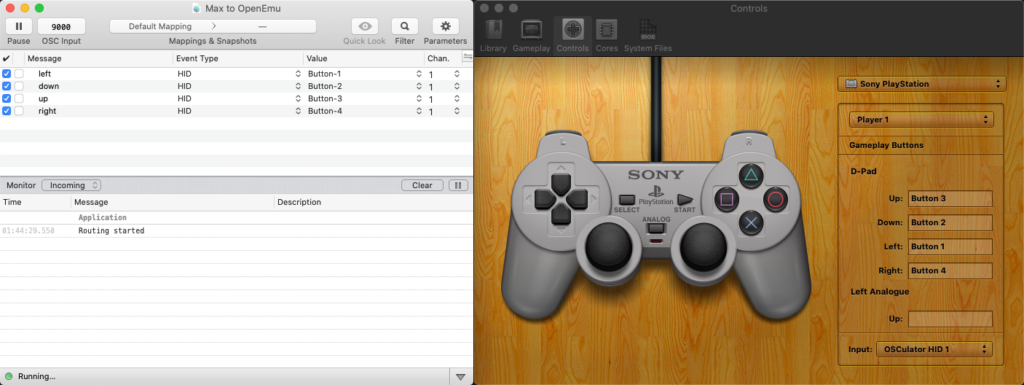
OSC encoded inputs in OSCulator are translated to HID output events, which are mapped to Up/Down/Left/Right inputs in OpenEmu.

Crisis averted. Back to the fun stuff.

Identifying Arrows

A key part of having Max play DDR autonomously is that it needs to be able to understand when an arrow passes the target area. Like the pulsing monochrome arrows in the target zone, the rising arrows also have a few characteristics: the centre pulses white, and the arrow shape’s hue rotates through a variety of colours.

As the arrows ascend up the screen, they pulse in time with the track.
When an arrow passes over the target zone, the internal colour inverts to white.

It took a bit of thinking (and a bit of experimenting) about how best to identify arrows as they pass by the target zone. I came up with a series of masks which I thought might help me draw out useful information (and ignore the background area around them).

Centre Zones
Arrowhead Outlines
Arrowhead Shapes (Filled)
Arrow Outlines
Arrow Shapes (Filled) — this is the one I ended up using.

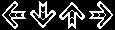
One initial thought was to watch the internal section of the rising arrow and wait until it goes white (using the ‘Centre Zones’ mask below to concentrate on this part of the arrow). This produced some positive results until I noticed in some of the more fast-paced songs that it only pulsed white on quarter-notes… which meant that fast songs with eighth-notes were overlooked. I decided that it might be best to use some of the other masks to try to identify a shift in from monochromatic to colour in the target zone.

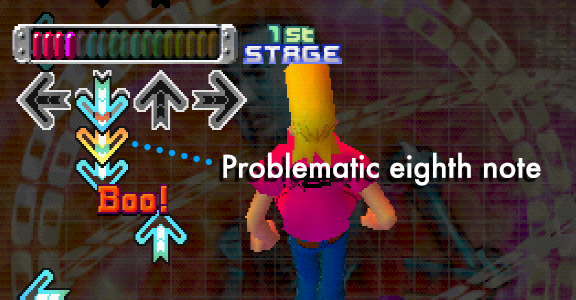
Watching the centre section of the arrows turn white is OK for quarter-notes, but eighth-notes pass by unnoticed.

The way I ended up identifying arrows with moderate success was by masking the arrow target areas, and watching for increases in chrominance. Tracking the white parts of the arrows meant that I couldn’t identify notes on off-beats, so switching the approach to identify increases in chrominance as the arrows passed the target should help overcome this obstacle.

The arrows in the target frame are pulsing, but they remain grey (which means that the R, G, B channels are roughly equal). When an arrow event passes through the target area though, it brings colour in to the frame. The amount of colour can be identified by converting the RGB matrix into an HSL matrix (jit.rgb2hsl), then piping the third outlet (saturation) into a jit.3m and watching the ‘mean’ levels of the single channel matrix.

Arrow area is masked, and the result is sent to jit.rgb2hsl to identify deviation from monochrome.

Watching Changes in Chroma

In the bottom right corner of the video, I’ve created a collection of multislider objects to illustrate a running history of how Max understands the arrows as they pass the target area. Note that we have spikes that indicate the highest point of saturation in colour that indicates when the arrows are most aligned with the arrow target areas. While we can use this information to identify when an arrow has aligned with the arrow frame with quite good accuracy, we (unfortunately) determine the peak value when the arrow moves away from the target area, which would mean that we would trigger the events too late. Perhaps a different approach would be to ask Max to trigger an event when it crosses a threshold, and use this downturn event to reset the state with a onebang (allowing arrows to be triggered again).

Limiting Input to Songs Only

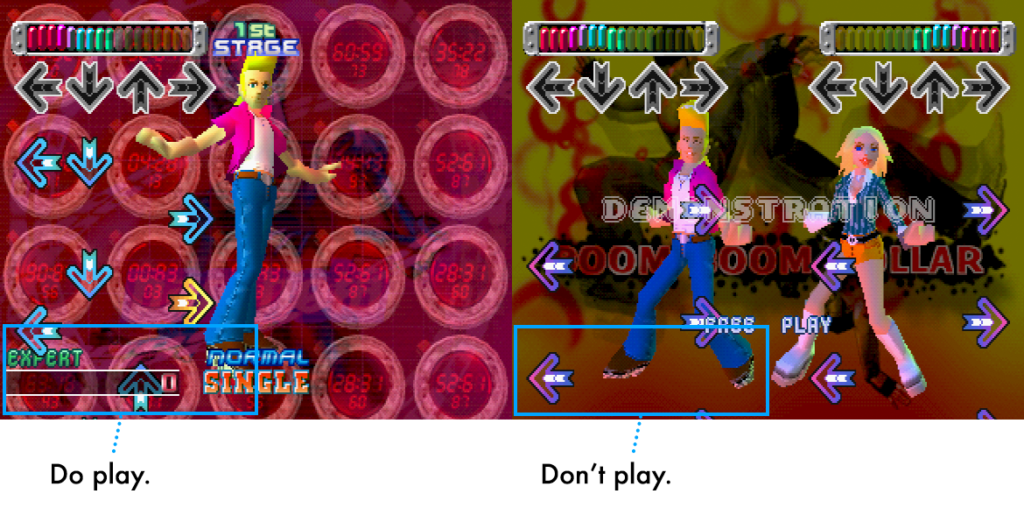
So that I didn’t have to juggle with starting and stopping Max from acting when it shouldn’t, one of the final touches I added was to disable arrow triggers if part of the game screen wasn’t in view. (This is why you might noticed Max go to sleep in between tracks.) Max will watch the score part of the screen to understand when to trigger arrow events. This ensures that arrows are not triggered on Demonstration screens, or other spurious instances of colour in the masked areas.

We know that a song is playing when two features are on the screen. The frame around the successbar and the border on the score.

Future Improvements

The video at the start of this post shows an example of Max playing some of the more difficult tracks in the game:

  • “If You Were Here” — Jennifer. [Paramount 🦶🦶🦶🦶🦶🦶🦶]
  • “Afronova” — Re-Venge. [Catastrophic 🦶🦶🦶🦶🦶🦶🦶🦶🦶]
  • “Dynamie Rave” — Naoki. [Catastrophic 🦶🦶🦶🦶🦶🦶🦶🦶🦶]

As can be seen, there are occasions where the timing of the triggered arrow events is not quite right. The system completes “If You Were Here” and “Dynamite Rave” fairly well, but struggles a bit with “Afronova”. This is mostly due to limitations in my implementation: as I’m purely using the screen to identify the events, the system gets easily fooled by rapid repeats when it can’t discern a drop in colour between frames.

Alternative Approaches

There might be some creative ways to get Max to follow the BPM of the track a little more acutely (and therefore quantize arrow trigger events) by performing some kind of beat detection on the music track. Alternatively, we might be able to determine the BPM of the track by watching the rate at which the target arrows pulse. Instead of just watching the arrows when they enter the frame, maybe it might be more robust to measure the optical flow of the rising arrows and time their triggers with a sub-frame temporal accuracy.

The Patcher

There are a couple of other things going on in the patcher if you want to download and have a snoop around. (Of course, you’ll need to do some setup with OpenEmu and OSCulator.)

Max-Plays-DDRDownload

Synthesising the THX Deep Note with Max and MC objects

The addition of MC to Max 8 added some handy ways to organise audio signals. One of the simplest benefits is the ability to pack stereo channels together with mc.pack~ 2 and process each of the channels with only half of the number of objects taking up space in your patcher (filtering stereo signals would previously require multiple biquad~ objects for example). MC also opens up some helpful ways to think about additive synthesis voices, richness of sound, and polyphony, and simplifies the patching needed to realise certain kinds of synthesised sounds.

One thing that is really wonderful about MC is the simplicity in which synthesised sounds can be made richer and fuller in the stereo space by modifying a group of oscillators’ frequencies and panning the individual ‘voices’.

Many softsynths — such as Native Instruments’ FM-8 — offer the ability to add more voices to ‘fatten up’ a sound.  The addition of extra oscillators combined with a small amount of detune adds a fullness to the sound that — before MC came along — would have required a fair amount of patching to replicate in Max. With MC objects though, this can be accomplished quite simply with MC object messages like ‘deviate’ and ‘spread’ eg. deviate 0.1 0 (to produce random bias values ranging between -0.1 to 0.1 for each voice of an oscillator) and spread 0. 1. (sent to the right inlet of mc.phasor~ to evenly spread the phase of a series of control oscillators, for example). Using these messages with objects like mc.sig~ can be useful ways to widen MC signals within the stereo space when mixing them to stereo with mc.stereo~ (or mc.mixdown~ 2).

Synthesising THX Deep Note using MC

Several years ago, on the 35th anniversary of its first screening, THX Ltd. released James A. Moorer’s score for the ‘THX Logo Theme’. Commonly referred to as the THX ‘Deep Note’ the theme is an instantly recognisable musical motif of swirling noise that coalesces into a D Major chord spanning 5 octaves.

The score describes the THX Logo Theme as thirty voices at random pitches between 200Hz and 400Hz.  Each voice moves slowly and randomly for a short time before proceeding to a predefined target note. The idea lends itself beautifully to MC. [Source: https://www.facebook.com/thxltd/photos/a.379994786929/10155235575876930/]

Building the THX Deep Note in Max is a great conceptual exercise, and drawing on the MC approach of thinking makes producing something like this quite straightforward. Here’s an example of how it might be done.

How does the patch work?

  1. An mc.sig~ object is given 30 voices all of MIDI pitch 61 (or C#3).
  2. These are scaled to the range 55–67 by an mc.rand~ object that outputs 30 randomly varying values — constantly shifting the incoming values from mc.sig~ up/down by an amount of up to 6 semitones.
  3. At the same time, 30 voices — the final chord, comprising 10 distinct pitches of 3 notes per pitch — are being broadcast by another mc.sig~ object.
  4. The two competing mc.sig~ values can be interpolated between by using the mix operator in a mc.gen~ object.
  5. The MIDI pitches are translated to frequencies with mc.mtof~. Keeping this as MIDI note numbers up until now is kind of nice as it allows you to think about things like detuning and pitch shifting in ‘cents’, due to the linear nature of pitch intervals in MIDI.
  6. Adjusting the main ‘Deep Note controls’ slider lets you play with the transition at step 4 in realtime. The values output by this slider object are fed into the Transition to pitch, Amplitude swell, and Pan function objects, which means that the different aspects of the sound can be independently styled while keeping the controls simple. The slider fades the sound out at either end, but bringing it in on the left side introduces the dissonant swirling noise, and dragging to the right starts the transition to ‘consonance’.
  7. The pitches produced during the transition are drawn on a stave with the nslider object, and an mc.scope~ shows the inter-pitch deviation.
  8. The sound is mixed to stereo with an mc.stereo~ object, where the placement of the different voices are subtly distributed in the stereo space by an mc.sig~ object that outputs 30 random values between 0.25 and 0.75 (due to the deviate 0.25 0.5 message).
  9. A few objects are used to roughen up the sound a little bit and boost the frequencies in the low end.

Here’s the patch if you want to have a play around:


----------begin_max5_patcher----------
5396.3oc08jsbqabkOq6WAJUoJmEck68kLujTwSVdvYbEmopoJeccKPhVjvF
DfF.T5JmJp7+v7CjmxGx7o3ujo2.3hHAa.BQJoKuhhMZftOq84b5Se3+3cWc
8jhOoptN52F8MQWc0+3cWcksISCW4+7UWuH9SSyhqrc65b0CES9tquwcoZ0m
psMWGAaZaYb8z4o4y9XoZZs6QCw.9sfahHX1sH5MQHj4SleG8s96Je0hz7LU
scTf9FSSrOb8.9dHPb85tVrpd295Zp9wkJ2XdcZtdz+VyE+mu6clecyoAhUp
rNARoEDobKrgIcCgn8Agr8CgnCAgShymc8MQWOpfYR0xp53Z0SGGTIfa0DSF
b.DS59AURWDSMjdWVQr8O7edvz3oEKVnLOicf9+97zpnGRyxhtKsTE8vbUdz
W70eUjtUUd7jLUxMQSVUGkdWTwRUtFsDcWYwhnoYoKmTDWlnu4541aINqTEm
7XT4pbS+tI5whUel9AmqTIQ0E5mW0J8PTOOtN593xzhUUQZjiFIWEEquPZdZ
cZbVZkJ41l4YVZtZZwpb6jk1AAxRSX.pSbCZ+HWzKRDY+jHfu0IqlnQG16d.
3eMNrtHuCVLrULhAYFVLJwwu0q4OX8SuLdgpVU9QGIbSnHPcIVIsAwnsJPHE
CcjJfkTgw8.TkhPfz4w4IE2cm8t5ovWidlV8Mmhj2BUUU7L0yj79O9PoteQY
wqxmNeRYwCUpxn400Kq9se9m+IL+9a0xr1+3y086yqm+o2mnTKeedQs58ZX6
8KltWoDxwv7HA07Fjhsbb8Qksj28ZRySSRT4cxYMtpufctJrDKsPpV8MludY
XPe30NlVgYSKxJJcCnd4ADkHAPICvEDL7FcShM9LliLMIITfT.vRDjxDL8Lz
LiFSzBnKzBhaQKDFeSiS5EVA+VDqH6Bo3EGf5ofEq.k8GqfdKhUDAgUPvAiU
fuEwJ7tvJ.lvt9LkMXjB3sHRg0ARQf8qp.FJNQHeKhSnAH9v.ClQQHdKhTHA
fTzqHOXjB+sHRA2ERghstXhzhO7AhTXuEQJn.3TPrgyoPeSZ9VmHEB0oSwYZ
auQI72j7I+w3DUjd1FEWGMonddjJOopKzDg6Vila8uDhn8GQcHCWFuXOUFMs
HutrHqSPAKvV9eJlYAIQ2weB7bPgw5YrDG2.IFDTxcx5P1Zt6dEiMF8EmbsX
5sYoKRepSwSGeGD5.AuFrdAHjdRrVrJqNc5737bUVU5r73rgQ9tKMqVUNqLd
47NAQjz4VMf5cfjxbxXaFusrz7EwkeuprpQShEq.bBhPlYAOZauuSyfbW7zc
CU0Z7jXO3Ib+C3EuY1ULaOyNPyasuuo9hmg2yRq1NHsc7GM80EFol4lCiuE0
sRU6Z0OwzrP5oxMl+viiYDf.KXHLfvDFiEH2xfDDU+Yh95DnvnQlpUHyXRt.
vwPqNZvA+0XJrqkQlj9CqhSBSJwE7AsRZZWRIr8P8QWHojNzMTTppdRq6B.h
.g.8.gWP5H6n.94fOkeg.+CENSPDF.5DpIThUcQST5c1wzqsLhdYWGaYVZsQ
dAZr3QJCZMatUHSB5MElH54tisiRmQ07quPoVF8WKpUlMFpZdb4xnIOFEOwX
QFEDMUeOU6eSaPcsPBwsOGLoyoGHs26E.AOdq5eHf+uopJxVUmVjGMcdQYRj
ID7cZKCS31oPerPvvda7IVdNrl427jYkh.TUQ8NqyP8VlEeozTcHx4+0hz5p
n4oylG8EQZZ5WVn0aW9YZ95o5+HJNOIJMupVEmDEmjToaP6ugpL59hzoJyFY
p8+ntXQT87RkJZhd3bLD212siQaxK2vlXr6vx+6zUv5CeBj9xy++Uw4QyT4p
x3rrGMH.M5vJxWpbaNrFMEEGoUNpG9nIZcjE2EoQfkphnpklMEduXFbWqU.s
LZBlOryTKlgv6Clg7xiY94e5e++8uLP+xX6ddqA93JCFZQw8JKZZVYwpkZ9o
03CiUt8UQI14ymT3CDBi0aEkPvYvaV8BOItMM83oFCv47.i1auYg3yhU.Gbs
vx3GbR7FsGU0w2q5bs.oUHmhjNZGTz6ECfnywhAIJsqeIpmhfQPTPlu58+CB
X815F1qKq2KiVj9oNgYjirIcf7wR2o8v0RunLse3ZLvsBVkIDZkljiXQzxTM
jpaYhp9AkJWyUB9y+ncEPh4u9v0QeyS+IzO+S+u+I721ac39vDvDtE2FfJ7y
fF70F1taLpBV4LE4bkUdKai0pX8I4cZUn4RxnpzD0lX28GnVSLSpR+QaOQF9
wmkmRa.re2pp5z6RmFaLi0dGCw2uo2p9wj3oOc7r6Q3PJHb6agqs6EWYWkVR
Ha0htTaigVpn.37Pg26n3gfzyvBtZ6N5bsVry6SpyLJLq2ZsPPxkMzwcCgdx
DzupJVL.5D9Lvu08pKdnfHrrYGiJsWf.cFTUlVUUjGmOM.4FWNx5BouIIrZg
Dm1okEoN8pfaAAChv8qjD8Bl0lGBU7GJxONpf4W+i1jKpciJf8.U.N+nhwvl
eAkZsEX.17i.xKp8SM6+XWY.iKV1NfiJFQV+0GEfKOq+u7qmFqmAQZaALFQ9
zmUEkntO0ZWg1OWsuue4e4K9KV+ihnz2y3FaMmo9U21e6GcooX6t+6Tt2KCH
QG5HF.FwHeq00g6LFZHOigKZftbRsWgPCAfWXmG94e5eGohmN2GDLS3Mphpx
JdH6Qq6BN+Ixd7CW2+Xa3rQAtcnd5WrMNTdIOp1ZcLO8EBWXdYt3aLf3ZHoW
nzq9f1sb7navrGXAI.adize6jgRxKNsqNJKZZlJtL.HQ3bfYPPBtm6XiYyZb
yqwjpsrTsTokIs6UQHPrigUvF.DitjNGDlsG9cfyGFhgDtQI70OT5WiAp4dG
LXBtrd5E.X5jM4.OPN.YTwK+9pELb3OOgTw..i9d3PG9A55PFE7WsQ.2jWKp
j8rMZ+xz7oYqRLaJBpIviKUkNCCSysaNhYuy9U81tPtFgYLTPfuU311LR+2b
HA+Ux1g3ClNhN3cCQbYir7eWa6WUp07esw+1HJ2A7Rg1cCg3OCZ.b+2LDwYH
rv+m17H6ySRqLuq8vodUtp6Hsw17LUocdo+.FWLd.VcwrYYpP1GNu6UH2NZz
qibJmMhG4zw93qqcPcl4Xca1NqPvCMm6KT+8OSqA5BscVGmL6MxqY6GGDYF+
ZfLeH2uiWtL6w6iyVoWfQHadwZdA8u3D+Klr4Ex+hxadA7uHTyKrv7Bwzu5c
pcPkN6w3L2QOU2PuOssP9E0vy5nIQSBf0p4zMQFfCDGJosQAczrGFzVkklnJ
Oti7XfiDJcYcOTdLR2hhD0ASSmVVn6197UrSt3tNknCWVCs+StgXiCjAxvCF
ZScjxymZYnPaa3x0UZiz73o0o2qhyVNOd6XfuOxhlPP.x0+ShVSjf3mSjlFm
MsUXk0HsNqLMYK7Dlr04Y4lfa5HrC13d5s54VhaGhIfM+g09.1hUAb.VEh.g
05wIZaFYDt8n3DRSvsmnG+H+XyV70+ZyHXeWyFNyHm2JvRixFhzmDwCnHrvv
W3hvxAf+ePKlWVDA6N8oaVHm4rSgM.yT5cNyeBZY2OnZL4Y1QRWJajD4PgyO
g9SloGvEebWgg6EhztLd52GBzRo1HwMfhnD8xFBN8iW4bu+5i6xtmndr31rW
vDNfXqN1fZdRzuKWEWppNR4+xSVYBrK+d6+Ic.RjWR55Ol4ybUVH5j3ZkxVv
c.fo3RSW09IVkGurZdQ8SgPSIhgJpRNe7vGxYoeAzjiegbvUNgSoCr2o7+nR
PM9n8TPfHNrj4bufXeqccdu7u4EXQU6A4HfPbzj93Dz.fW5k5PotJepMmEOZ
NGgbtBP8IXMeSWARJVDmlusKFFGAppUK+3mboiALTCLvj9GODxQO0VM+2ydz
DvA0LUdxlO23jDaNjT8LOHuY2OfvPgf.nbIGBfDqaLRp.u9GeGoX1l80zDWJ
Xv0+36HmnwxZWFoT.GQX1i9OUKP09iz2QgT6LY6S0UP.bmf0aa903Vf.LYnf
4jX.8mFsOKff1R7EBKfOze39Wj.fX74H27+0gbZZYbrufdQZKrW8PBG9p6.0
9qMGOsNMzh.29vj.5ulMD6UGb+aBgZS8qdAICvrKzkRc9QC9VSF8Bbwq1qMW
atEecnw997hIUyicStlpBZSjIBOOJgHzvCrsUust8kqpOia11W0Y1PSc0MTs
5ZWR3CFvIMZDy99vW5V3NgruLKcuQb3ducC22LJqaA6fWaqqqmu.6gJwsrNh
xjZ+PjL.gSv1lfLAEKwHpff3M8iZJ4CHJRxHtVuEBP5aCQILAT6AiuiP.fKA
l0uwXazT0MA0F.voHAPuJunsiDABos6AK3Xpq9R.HZqJgPFDPDr1k8gTgdn3
Ll17ABTZg.nuK5ggxYsOxFv.Hv..w1SDTpsSAhvTo1.CViUL7M+G10ShDvvL
Nf.gZqQ78DuwXKjb2nKYLjzL40LYjlmYCnv4BFkYM3A.jXFFosOR.fsOQNkH
IF.kvPDWzwoaB4M.tGNzlWYHRnN5HGgwHfGQ4hiLPOEZP6s8SpwDZDFGvo.o
zyKP23Y1zSJBxwZrqlhP3BG9QKGyQHAQy..ksz6s3KXdpyFHG.qgEpEGZmrn
NniBDCngNJyMM7yyM4hjqs6686gicT0O96WXpQCqRTQe8CprrtzU5RXJgq1a
HI8WUITdITURck7qWdubf7Wed4rEGHugEDroVQfvoGhiAXrV3QKeCa3pgOyK
Gz1+zH0qYb0pBz5VzRDFsXFkPXsaBHrjqEx4MpGHBAjfzRPVoUoSigaLcb4M
NXwVKJatEqv39z2vATJVq9iIvboSeCiq0QiXMBzMhc7sD7rNhYzmz9iXT715
PwQxkx+JChgZvCgjZhLlMq8jCHZKvySPtCDZogbTWDtMEeHP6Y5ntDTBULF4
QQapTzjMECJgJ3s0nqAmOEfKZbIMAZNc1SQ+NiaTUZqyCHqkaqGnPx.9Rm.+
pyyV6QFxZ.dPXATSsIm3vBj9WM8DjWcHAKWPv3flf2BaBRU+4DDu9XDbkCEs
vP7p5hYZqV5dC0ZK4DM0g7ADzCwkphwExwlecEwSt49tX9c3j4Qz2caot7d0
sFRS67993xbskfGtCc.XbnSSFxWbEM4Ka3PVmdlC6zVTMHU6IhqSubPOn4dK
V2tTN1N0qhuWk7w355xzIqpUq+qJO10idMXO8RpE20zbS6aBSYE4y5DCuUuW
noX1bwowX+ctpyUf2yA685UyKJqCevZvQ66QsJOstp9QG0f3ttkeq4sQSswh
5h6BJT39bRb.msBt70mxx3GBBnwtkHnrdqajKdaFD7l5wCC2ePl+Zb+NXgXN
jOk8o8e2NtXIp9gO7zAIM61OK4s8cWs3f2LV76gUOC8PL3mBdkQbWj9oneAL
fxpk4Lfar4o+NKSnWXB7LUtl.eri8TC0s4K8BBD1ePcT1f1lPEFWGuqAJ14s
qvSusAJ2klotWUV4KcTvVS.hWtbi1uZq6xfA+NWREKtYcao4t1vqaqTce5yd
15GdoFKVqQgqJc1n7o1JidS11WluJss.WXopsSMKsyXdiqhK5yyXC4Zs0MaD
MXegXl3T23JGOzMBGrMKoyJl98pjssBx8sh3xRUkJuts5Zs95Ip6h0zgOtY0
5xt8b6qC6TBz24psFq86KSiyVCFlP7VjalHaScrg90OjlPJ3994YKXx1k73k
6618e2LdfqZxX6UUShKMzNug3n1qVWTjs80VemYp6p8WeYpl2bGDZcwxNtZY
5r4cc2tZyZmOd6kpzFs5t7GMNH7QiY76zw3rLuX+NivmhySWDWqpSczCsKMs
W04Ux7pokEYYaC2tKc+9tjI.iSUOjlTOeqRCi8R5aHcYCi00qI6IoyTU06zX
c7rpcZp0x7Maa0Duz9GqUKVloglc5gV5Q6mi1IgGp78rg8aKTw5uLc2V3eSE
p6bkN2Jmq1VA6+ckqLpZVIQyCVFWWTZq.sqOzoM0tvDe4op1VPRl5qPS0M03
va2Z.1WXGu5fJuENaMcaRcS88aKkCGZ44qdlmrWuysrqe5a57zUMKQMTb6VK
asCpU2qEKi.swc4vfuCf8Ab8Yqa0Cfm2Avu08bnUsOaHmux3a6FUssigbbVq
wXAfb.G.4vdyfbB.s3cMwKw.kAfWvG.uPeyfW1HHlGAw3MtWbBrKv2RnEzQE
i.iEdA8lAuX9tSHP9Er6HyfomfxWRuW4YC6DMqWdvU5sSaSONDJopXU4zFzr
WWWzNvf1Nm5z7VCn+l1ULZ145fnK8epvCcpn0CEgdQmJzPmJjWbrBrOXkW1o
BpOSE3AlJMM2FUZuavOTpcg0EA6eXk56UO59NLmnMoGfwB30iYgR4O++Dstb
S+PZ87nu7OD48x51Oj27c98MQ+Q0jxUwkOZNRCn9VP8N4ud0IA7MEf8gssVA
GpYW5qGA8bFLylSGsQpKseFc3ZZ5ynBgOT7.Fp1IzINVx.FKwnLTPTHCEYTF
pPvf1Jd8oOVlrvMfwZTPgnPPg6B8EkItfjAOGC9Nni1AGbNFbLY+CN5DGbVH
CtYuJNcgeLLDoDvXvMsC15PbtnQYrng.VnQACFD0BOJppwAoptYFcZiEIDNC
64vdjFK3wFKJbTFKQHvkbTTfRBY4NaEY3zGKZPzK5nvySCR8XCl9DGKYvv0I
OVrffK1nrPNCGjV9QgOjQCQ9h.Gsw5LwavgmOSW4AQuXiBeHmDjsOzwPVlGt
0FmLbIBg2fOJVaHAAY65nPtjgwFxGkwJHUTxQgbIChkWhFswBdlfqfTQQ2Vv
XipK+IM51usBN5nSGCg.TPta25T9oMVvfzYgGCcVgYZJZLVllPCMNLm5HQCQ
gEeLzgvAmKFvfVGyBSmJKAmetnSbQv96cpCk.DpWrm7HgCV38jGpvrsYakuK
R257NBMacpsb8ZqrVPBh09wwNVPAMe4jWhXfEjtmwIphgshH3PqHN1Q.KLeH
fgNcNQNfPL4ZLh4BOjkq4igmSAEHIt7rwZgeQhgLkc1BWl0e1iY9JczFoiCT
iggBAEhhQwi2fB7BaLL9mEh5bA7rs8I6DtjVNe7oAkgv4OJwfIjAhNFLiT94
hYTFhDlj+h3cn8qtl.bYaThQBHnXjHFkkA.AsjNXT15B.6LhCChdwGE3JHiz
AOWp1kNB6bZDLixNmAgcN9AO+jGb3Ccvtm2.aJjruSYfI4Pd2+7c++DAEIoB
-----------end_max5_patcher-----------

For fun, try disabling the ‘Enable/disabled detune’ (step 10) to hear the difference between strictly tuned notes, and Moorer’s subtle detuning. The detuning makes it sound more rich and organic. Also, try changing the final resolution chord to match Moorer’s score (step 11). [Interestingly, the score depicts a high 89 / F5 which seems to not be present in the theme itself.]

There’s a lot of nuance to the THX Deep Note, and the end result made with Max here is similar to the original, but there are still some subtle differences. Aspects described in the score (such as how “each note moves slowly and randomly”) sounds a little more like sinusoidal oscillations in pitch in the theme (as opposed to the way they are shifted randomly by mc.rand~ in the Max version here). Rethinking the way they move randomly might be a fun exercise using mc.cycle~. There’s also a non-linear ascent to the final chord in the original which sounds like an acceleration towards resolution. Playing around with the function objects controlling the ‘transition to pitch’, ‘amplitude swell’, and ‘pan’ might be good places to start experimenting.

Links:

Controlling Max with Messages

This topic has come up several times on the Max forums, but I never remember what to search/where to look to find the various ; max messages you can use to issue commands to Max. Typically, Gregory Taylor recommends that searching for “messages to max” (in Max’s search box) will point you in the right direction to find the ‘Controlling Max with Messages’ vignette. There are several other useful resources about messages to Max, so I am echoing them here for future reference.

The Technical Notes section of the Max 8 Documentation not only contains links to a list of ; max messages, but also contains a handy collection of things such as messages to control MSP and Jitter (links below), and lead me to re-find a few other things that I tend to forget about (like being able to send messages to a receive object by name).

There are times when it can be useful to send messages to receive objects with a standalone message too. Messages to receive objects can be sent by replacing ‘max’ with the name argument of the receive object, ie. ; foo bar sends the message bar to receive foo. Placeholders also work here, eg. sending bar into ; foo $1 will have the same result.

A side note: the Technical Notes page also includes several links to ‘functional listings’ of objects grouped by their ‘subject’:

This is a useful way to find related objects other than via their help patches.

Max objects in HTML/CSS

This is a post with no point other than to share some CSS styles I made for recreating the appearance of Max 8 objects in a web browser. I’ve been planning to post several short entries about Max ideas, and after using a square bracket notation to convey Max code in text [like this] (when posting on the Max forums for example), I tried recreating them in HTML and CSS to help make text-based description of Max code a little more intuitive.

These styles reproduce the vanilla styling of Max 8 objects, messages and comments. With the exception of bubble comments, all elements are displayed in their unlocked state like this:

sah~ jit.pwindow @size 1280 720 qmetro 20 @active 1
replace drumloop.aif read bounce.mov startwindow
-40 2.71 C-2
Load sample then hit spacebar Ensure dac~ is running Use localhost/127.0.0.1 port 9000
Click and drag in the multislider Switch between fullscreen and windowed Turn on metro

Usage

Max objects can be created with any semantically appropriate inline/inline-block element, eg. <code> or <span> — the rules in the stylesheet will set display: inline-block; on the element used. As the elements are inline-blocks, they can be placed inline within text like this.

Give the element a class of "max object", "max message", "max number", "max comment", "max comment bubble", (or "max comment bubble multiline") to produce the desired object. (See Examples below).

I’ve also sketched up a jQuery script that adds an adjustable number of inlets and outlets based on the elements’ data-inlets and data-outlets attributes.  By default, objects are given an inlet and an outlet, unless specified otherwise by adding data-inlets="5" and data-outlets="2" attributes. Messages, numbers, and comments are given their standard number of inlets and outlets without having to explicitly specify them. Inlets and outlets can be suppressed though by adding data-inlets="false" (or data-inlets="0") and data-outlets="false" (or data-outlets="0").

Examples

metro 125
<code class="max object" data-inlets="2" data-outlets="1">metro 125</code>

vst~ 8 8 VCV-Bridge.vst
<code class="max object" data-inlets="8" data-outlets="14">vst~ 8 8 VCV-Bridge.vst</code>

jit.bfg
<code class="max object" data-inlets="1" data-outlets="2">jit.bfg</code>

cpuclock
<code class="max object">cpuclock</code>

p adstatus_settings
<code class="max object" data-inlets="0" data-outlets="0">p adstatus_settings</code>

read ducks.mov, bang
<code class="max message">read ducks.mov, bang</code>

replace drumLoop.aif
<code class="max message">replace drumLoop.aif</code>

"CC 4" $1
<code class="max message">"CC 4" $1</code>

74
<code class="max number">74</code>

A#5
<code class="max number selected">A#5</code>

0.98
<code class="max number">0.98</code>

0.0016328
<code class="max number selected">0.0016328</code>

A regular comment
<code class="max comment">A regular comment</code>

A 'bubble' comment
<code class="max comment bubble" data-arrow="left">A 'bubble' comment</code>

For completeness, comments can also be forced to be multiline with the addition of the ‘multiline’ class, like this:

A 'bubble' comment that
spans multiple lines.
<code class="max comment bubble multiline" data-arrow="left">A 'bubble' comment that<br />spans multiple lines</code>

(As bubble comments are displayed as ‘inline-block’ elements, multiline bubble comments must have line breaks in them with <br /> element as shown above, to force the text to wrap over multiple lines).

Bubble Comments

Changing the data-arrow attribute can also be used to change the side of the bubble comment’s arrow like this:

A left arrow 'bubble' comment
<code class="max comment bubble" data-arrow="left">A left arrow 'bubble' comment</code>

A top arrow 'bubble' comment
<code class="max comment bubble" data-arrow="top">A top arrow 'bubble' comment</code>

A right arrow 'bubble' comment
<code class="max comment bubble" data-arrow="right">A right arrow 'bubble' comment</code>

A bottom arrow 'bubble' comment
<code class="max comment bubble" data-arrow="bottom">A bottom arrow 'bubble' comment</code>

A multiline left
arrow 'bubble' comment
<code class="max comment bubble multiline" data-arrow="left">A multiline<br />left arrow 'bubble' comment</code>

A multiline top
arrow 'bubble' comment
<code class="max comment bubble multiline" data-arrow="top">A multiline<br />top arrow 'bubble' comment</code>

A multiline right
arrow 'bubble' comment
<code class="max comment bubble multiline" data-arrow="right">A multiline<br />right arrow 'bubble' comment</code>

A multiline bottom
arrow 'bubble' comment
<code class="max comment bubble multiline" data-arrow="botton">A multiline<br />bottom arrow 'bubble' comment</code>

Unlocked Patcher

Lastly, if you want to add a patcher canvas to your page, use a block element (eg. <section>) with a "max patcher" class like this: <section class="max patcher"></section> — and nest your elements inside it, eg.

jit.hello

<section class="max patcher">
<code class="max object">jit.hello</code>
</section>

Patchers can also have a data-zoom attribute if you want to increase/decrease zoom levels. Acceptable values are 25%, 50%, 75%, 100%, 125%, 150%, 200%, 300%, 400%. Treat this as a bonus feature that may not work in some browsers (Firefox, Opera).

jit.bfg

<section class="max patcher" data-zoom="200%">
<code class="max object">jit.bfg</code>
</section>

Download

Download the CSS and JS files:

and add the following to the <head>:

<link href="path/to/maxobjects.css" rel="stylesheet">
<script src="path/to/jquery.js"></script>
<script src="path/to/maxobjects.js"></script>

VCV Rack and Cubase

[This post was written using Rack v0.6. The following will continue to work until Rack v2, however this information is now largely obsolete given that VCV Bridge is deprecated and unsupported as of Rack v1]

I recently started using VCV Rack. Rack is a cross-platform open-source modular synthesizer that aims to model Eurorack standards in software. While it is yet to hit version 1.0, Rack already has a sizeable number of free (and paid) plugins that extend functionality of the software, and an active community. Rack runs as a standalone application, but also plays nicely with other DAWs.

The Rack manual outlines how to use it with several audio applications, but details for integrating it with some of the software I often return to—Max and Cubase—was missing from the Bridge page at the time of this writing. It seems that some updates to the manual (detailing how to use Rack with Cubase) are waiting for review in GitHub, but the steps listed don’t appear to work with Cubase on macOS.

In the meantime, though here are the steps I have used to get audio from Rack in and out of Cubase. A post about using Rack with Max will follow. [See above]

Continue reading →

Structuring JSON data with the [dict] object in Max 

{
	"perceivedComplexity": "beastly",
	"actualComplexity": "manageable",
}

Working with setting and getting content from dictionaries in Max seems straightforward enough, but trying to group data into well-structured form can be a little tricky.

Structured Data

Recently I had a need to create a way to store some fairly complex data in Max. I wanted to map out and find similarities in a bunch of audio files. I’m not a computer scientist or a real programmer, so I had no idea how I should do this or how I should store this information in a manageable way. [As it turns out, I needed to create a hash table.]

Traditionally, the coll object was the go-to object to do this kind of stuff (and still is to an extent). It’s a simple way to store a list of values at a numerical (or symbolic) index.

1, 100 72 64 forward 7.43 delay 85 0;
2, 60 160 62 forward 5.0 bypass 51 1;
3, 82 10 114 backward 0.2 delay 15 1;
4, 155 97 98 backward 8.2 delay 99 0;

Send the coll object a 2, and the corresponding data (60 160 62 forward 5.0 bypass 51 1) will come out the first outlet.

When trying to encode lots of data though, a more descriptive index would be more helpful.

While coll supports indexes that are symbols, I was keen to use something that allowed me to look up or retrieve particular ‘atoms’ of the information I was storing. With coll, if you request the data stored at an index, you retrieve all the data stored at that index. As coll data is stored as a list of values, the order of the data stored at that index is important, and it can be a little difficult to see what each value represents. Furthermore, as I was interested in storing and retrieving data based on some kind of shared similarity (ie. separate arrays of data that should be grouped under the same ‘index’) I wanted to store it in a more descriptive and extensible way. What I needed was something like an associative array.

Associative arrays store every piece of information as key and value pairs. This data structure goes by many differing names (dictionaries, hashes, maps, symbol tables, hash tables, collections). In the JavaScript world these kinds data storage structures are referred to as objects. I’ll refer to them as objects for the time being. (Just to confuse things more, key-value pairs are also sometimes termed name-value pairs, index-value pairs, and attribute-value pairs.)

The key would describe the bit of information I was interested in storing, and the value would be the number/setting/value representing that information.

Essentially, objects represent structured data like this:

{
	"name": "Alex",
	"sex": "male",
	"age": 35,
	"coffee": "espresso",
	"coffeeTimes": [7, 9, 11, 16]
}

An example of object notation.

keys sit on the left, values on the right. There’s a colon after each key, and a comma after the first to the penultimate key-value pair. keys are strings, and all strings are surrounded by quotes (eg. "coffee" or "espresso"), and arrays are a list of comma separated values in square brackets (eg. [7, 8, 11, 16]).

The cool thing about object notation is that values can be strings, numbers, lists/arrays, or even objects themselves. Even better is that you can insert a new key-value pair at any point within your object and it won’t break anything, because you retrieve values by their key (in contrast to coll where you’d have to keep track of where the data value you were storing was in the array of values stored at that index).

Combined with arrays, objects are very flexible ways to store and format data. Scott Murray’s D3 Tutorial chapter on Data Types illustrates the power of objects and arrays really well: “You can combine these two structures to create arrays of objects, or objects of arrays, or objects of objects or, well, basically whatever structure makes sense for your data set.”

What do ‘arrays of objects’, ‘objects of arrays’, and ‘objects of objects’ mean?

Well, many things. If an array is a list of items, and an object is a collection of named properties grouped together. You could combine them in ways to:

  • create a list of data structures that were all related in some way and assign them all to one keyed list (and access info about each one by its index in the array); or
  • nest specific bits of information within the context in which they are relevant; or
  • have a collection of properties that had their own groups of sub properties, and so on.

Example 1:

{
	"animals": [
		{ "name": "Alex", "sex": "male", "age": 35, "species": "human" },
		{ "name": "Benny", "sex": "male", "age": 3, "species": "cat" },
		{ "name": "Mench", "sex": "male", "age": 6, "species": "cat" }		
	]
}

The animals key contains an array of objects.

Example 2:

{
	"series1": [ 0, 1, 3, 7, 15, 31, 63 ],
	"series2": [ 1, 4, 9, 16, 25, 36, 49 ],
	"series3": [ 1, 2, 4, 7, 11, 16, 22 ],
	"series4": [ 1, 1, 2, 3, 5, 8, 13 ]
}

An object whose keys are all arrays.

Example 3:

{
	"name": "Alex",
	"sex": "male",
	"age": 35,
	"coffee": {
		"type": "espresso",
		"specs": {
			"shots": 2,
			"milk": 1,
			"sugar": 0
		}
	},
	"coffeeTimes": [ 7, 9, 11, 16 ]
}

Note that the ‘coffee’ key contains an object with two keys (‘type’ and ‘specs’), and the value of ‘specs’ itself is an object.

Essentially, [] indicates an array, and {} an object. In JavaScript, you access objects’ values by their key, and arrays’ values by appending their numerical index (starting at 0) in square brackets. If an object is contained within another object, you use ‘dot’ notation to indicate the ‘path’ to the desired named element.

age					// Returns 35
coffee.type			// Returns "espresso"
coffee.specs.shots	// Returns 2
coffeeTimes[2]		// Returns 11

Retrieving properties of keys and arrays in JavaScript.

JavaScript Object Notation

JavaScript Object Notation (or JSON) is a specific syntax for organising data as JavaScript objects. Essentially keys are wrapped in double quotes, as are the values if they are strings/symbols.

{
  "firstName": "John",
  "lastName": "Smith",
  "isAlive": true,
  "age": 25,
  "address": {
    "streetAddress": "21 2nd Street",
    "city": "New York",
    "state": "NY",
    "postalCode": "10021-3100"
  },
  "phoneNumbers": [
    {
      "type": "home",
      "number": "212 555-1234"
    },
    {
      "type": "office",
      "number": "646 555-4567"
    }
  ],
  "children": [],
  "spouse": null
}

[From the JSON entry on Wikipedia

Note again that the value stored under ‘address’ is itself an object that contains its own key-value pairs, and that ‘phoneNumbers’ contains an array of objects.

Dictionaries in Max: The [dict] object

The dict object emerged in Max 6 as a way to store structured data like this. As the term ‘object’ in Max refers to elements within a patch that perform a function, object-like data structures are referred to as dictionaries in Max.

{
	"key": "value",
	"anotherKey": "anotherValue"
}

Why are dictionaries good?

Apart from the fact that data can be structured in a more meaningful and readable way, the order of the key-value data pairs they contain doesn’t matter. As alluded to above, in the coll object, changing the order of the values in an array would likely break something in your patch (as the position of the items in the array carries some kind of associative meaning), whereas in a dictionary the order doesn’t matter as you request the value stored at a key (as opposed to the nth item in a list).

In a coll:

1, 100 72 64 forward 7.43 delay 85 0;

… is different to:

1, 64 forward 100 72 7.43 delay 85 0;

Whereas in a dict:

{
	"key1": 54,
	"key2": 95,
	"key3": 8
}

…is equivalent to:

{
	"key1": 54,
	"key3": 8,
	"key2": 95
}

Building dictionary content

The dict object allows us to programmatically build up content in a JSON-like way. There are a few ways of setting content in a dict object.

set, append, and replace messages allow you to:

  • set a string (symbol), number (int/float), or array at a particular key;
  • append values to a specified key to turn it into an array (or insert the key and value pair if it does not existing within the dictionary); and
  • replace the value at an existing key (or insert the key and value pair if it does not existing within the dictionary).

For example, the message:

set tree 4

Creates the following in the dict:

{
	"tree": 4
}

…and sending the message: (if the dict already contained {"tree": 4})

append tree oak

… would result in:

{
	"tree": [4, "oak"]
}

(We’ve appended a value to the key ‘tree’, so it now contains an array of two items.)

Message:

replace tree none

… changes dict‘s content to:

{
	"tree": "none"
}

(Replace the value at key ‘tree’ with something else.)

Before we get to nesting dictionaries within dictionaries, let’s look at how to retrieve content.

Retrieving content from a dictionary

{
	"name": "Alex",
	"sex": "male",
	"age": 35,
	"coffee": {
		"type": "espresso",
		"specs": {
			"shots": 2,
			"milk": 1,
			"sugar": 0
		}
	},
	"coffeeTimes": [ 7, 9, 11, 16 ]
}

There are a few methods that allow you to get information from a dictionary: get, gettype, getsize, and getkeys. Given the dictionary above, the following is an example of what gets output with these get methods.

Method Example key Output (key and value)
get name name Alex
sex sex male
coffee coffee dictionary u504001192
coffee::type coffee::type espresso
coffeeTimes coffeeTimes 7 9 11 16
gettype name symbol
age int
coffee coffee dictionary
coffeetimes coffeeTimes array
getsize name name 1 [ie. 1 string]
age age 1 [ie. 1 int]
coffee coffee 1 [ie. 1 dictionary]
coffee::specs coffee::specs 1 [ie. 1 dictionary]
coffeeTimes coffeeTimes 4 [ie. 4 values in the array]
getkeys [outputs a list of all the top level keys]

Note that to access nested dictionary content (eg. ‘specs’), you use a double colon separator (::) — ie. get coffee::type.

So we can retrieve nested dictionary content, but how do we set it?

Setting key-value pairs is easy, but setting nested dictionary content (ie. a dictionary at a key, or an array of dictionaries at a key) requires a few little steps to do correctly. Let’s build a complex set of nested content like GeoJSON data as an example:

{
    "type": "FeatureCollection",
    "features": [
        {
            "type": "Feature",
            "geometry": {
                "type": "Point",
                "coordinates": [ 150.1282427, -24.471803 ]
            },
            "properties": {
                "type": "town"
            }
        }
    ]
}

[From Scott Murray’s Types of data]

The setparse message

There’s not very much about setparse in the Max help patches, but setparse is one of the most important messages when trying to construct dictionaries within dictionaries using Max messages.

setparse allows you to set content as a dictionary at a specified key.

Let’s go back to a simple example:

{
	"name": "Alex",
	"sex": "male",
	"age": 35
}

The syntax for setparse goes like this:

setparse coffee type: espresso

The first word after ‘setparse’ is the key at which you wish to add some dictionary value. If the second word has a trailing colon (eg. as in ‘type:’), it creates a dictionary with that key (‘type’) within the first key (‘coffee’). Re-read that if it didn’t make sense.

If you list a value after the second word (eg. ‘espresso’), it sets the value at the second word’s key (ie. the value of the nested dictionary’s key).

Namely, the dictionary would now look like this:

{
	"name": "Alex",
	"sex": "male",
	"age": 35,
	"coffee": {
		"type": "espresso"
	}
}

You can specify as many words with trailing colons as you like and it will create those keys, eg. the message:

setparse coffee origin: roast: age:

…would create:

{
	"name": "Alex",
	"sex": "male",
	"age": 35,
	"coffee": {
		"origin": "*",
		"roast": "*",
		"age": "*"
	}
}

…and Max will store placeholder text ("*") at those keys (if no value is listed after each key). Note though that the type key disappeared. When you set content (and this includes setparse), it overwrites existing content at that key. It is sometimes best to create a key with setparse:

{
	"name": "Alex",
	"sex": "male",
	"age": 35
}
setparse coffee type: espresso

… then append the elements one at a time like this:

append coffee::origin *
append coffee::roast *
append coffee::age *

This will retain the four keys (type:, origin:, roast:, and age:)

Making a key store an array of dictionaries.

Lastly, if you want an item stored at a key to be an array of dictionaries, there is a cool thing you can do to achieve this (that, as far as I can see is undocumented in the help patches).

Let’s try to create this structure:

{
    "type": "FeatureCollection",
    "features": [
        {
            "type": "Feature",
            "geometry": {
                "type": "Point",
                "coordinates": [ 150.1282427, -24.471803 ]
            },
            "properties": {
                "type": "town"
            }
        }
    ]
}

Here is a list of messages (with a comment explaining what each does):

set type FeatureCollection // create a key called 'type' and assign it the value 'FeatureCollection'
set features // create an 'empty key' called 'features'
append features // this is a crucial step - this turns features' value into an empty array
setparse features[0] type: geometry: properties: // creates an object with three keys under the first 'features' key of the array
set features[0]::type Feature // as with the last step, we need to ensure we address the items with square bracket notation now that it's an array


setparse features[0]::geometry type: coordinates: // add a key with a dictionary value (with its own two keys) to 'features'
set features[0]::geometry::type Point // set the value of 'type' within the geometry dictionary
set features[0]::geometry::coordinates 150.12825 -24.471804 // set the value of 'coordinates' within the geometry dictionary to an array of floats


setparse features[0]::geometry type: Point coordinates: 150.12825 -24.471804 // or the previous 3 lines all in one step

setparse features[0]::properties type: town // create a new key 'properties' and set its content as a dictionary

Optional: should you wish to extend the length of the ‘features’ array, try:

append features * // append some dummy data to the 'features' array, then...
setparse features[1] type: geometry: properties: // add the keys
append features * // again, extend the 'features' array
setparse features[2] type: geometry: properties: // add keys to the third item in the array
append features * // and again, extend the 'features' array
setparse features[3] type: geometry: properties: // ...you get the idea.

Building GeoJSON data example patch

A comprehensive tutorial (aside from this vignette) from Cycling ’74 is still very much desired, but in the meantime check out the help patch below for some examples of how to create complex dictionary structures.

Perspective Simulation

I was recently watching some videos about using ‘displacement maps’ in After Effects, which is a way to give 2D images the appearance of being 3D. It’s a beautifully simple idea and I wanted to see if I could recreate this effect in Processing.

In short, the 3D appearance is simulated by offsetting the position of each pixel by some (varying) value. The offset amount is dictated by a depth map, which can be as simple as a series of greyscale layers that represent ‘planes’ of extrusion, much like how elevation is represented on a topographical map.

The following video simulates a moving perspective, where the only source material is a still image, and a greyscale image representing topography.

This effect is achieved by using the brightness of the pixels in the depth map to offset the location of pixels from the input source. Sarah created a detailed depth map for this (below).

George Hodan - Face of the Man
Input Source, Face of the Man by George Hodan
Depth map (detailed)
Depth Map (Detailed)

My initial approach used a simple lookup of the depth map to offset the pixels of the input source to create the output. This is a fairly efficient implementation, but produces a low-quality output, as using a one-pass lookup to extrude points can leave some pixels in the output array blank. Why? Because bright areas can offset pixels by a large value, and dark values offset by a small value. Some pixels in the source input can therefore be mapped to the same pixel in the output (and therefore some output pixels are left unmapped).

You can see the result of this in the video below:

Download the PerspectiveLite Processing sketch.

Additionally, a single iteration through the list of pixels can cause pixels later in the array to overwrite any previously set pixels (which has the potential of bringing the top lip in front of bottom lip when shifting the perspective upwards, for example).

A higher quality result (as shown in the first video) can be produced by deducing which pixel is likely to be mapped to a specific point in the output — this also allows brighter values in the depth map to take precedence. This is done by walking through the output array, and calculating which pixel (given the magnitude of the perspective transform) meets the conditions of that amount of offset. Stepping through the pixels on the depth map (from 0 to the maximum offset, multiplied by the brightness of the pixel in the depth map) also lets you calculate which pixel from the input should be the frontmost (in the event that two pixels are mapped to the same point the output).

The following sketch demonstrates this approach. This implementation is a bit too computationally expensive to run in the browser at useful frame rates unfortunately, but you can download the Perspective Processing sketch to play around with offline.

Rainbow Apple Logo from WWDC2014 in Processing

Watching WWDC 2014 recently, the Apple graphic that was projected behind the presenters caught my eye.
WWDC2014
I was playing with Processing before watching this, so I started thinking about how such a graphic could be created. If a low resolution image of the Apple logo was used as input, the brightness of the pixels could be mapped to the size of the squares.

Here’s a rough Processing sketch to recreate the projected ‘rainbow’ Apple logo from http://www.apple.com/au/apple-events/june-2014/. The source image has a gaussian blur applied to it before downscaling to soften the gradient. This has the effect of scaling the squares adjacent to the logo’s edge.

[processing]AppleLogo[/processing]

Fix .mxo Max externals displaying as a folder

Under Mavericks, I’ve noticed that quite a number of Max .mxo objects show up in the Finder as folders. Max won’t load these even if they’re in your search path.

Vade wrote about this back in 2006 — MXO externals showing up as Folders in Max/MSP? — and offered a solution.

This fix is easy for the odd external, but cumbersome for a collection of objects. Here’s a Max patch to fix up individual/multiple objects quickly.

Require’s Jasch’s [fscopy], [strrchr], [strcut], and [strcat] objects.
Available from: http://www.jasch.ch/dl/default.htm

Problem: Max objects showing up as folders.
Fix: Drag a .mxo folder into the dropfile object in the following patch.